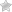Расчет площади треугольника: простые и доступные способы

Для вычисления площади такой фигуры, как треугольник, существует несколько способов. Кроме изучаемого в школе способа найти искомый параметр помогают другие методы.

Классические методы расчета

Отличие в разных формулах заключается в исходных данных. В них используются различные элементы треугольника. В задачах не всегда есть возможность выбирать вводные величины. Базовая школьная формула основаны на знании длины одной из сторон (a):

• из противоположного угла на известное основание опускают высоту (h);
• измеряют ее длину;
• произведение двух известных величин делят надвое и получают площадь треугольника.

На заметку! Запись этой формулы:

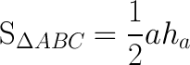
Также в школьной программе часто используется способ расчета площади произвольного (в т. ч. равнобедренного) треугольника на основании известного угла (α) и длины примыкающих к нему сторон (a и b):

1. Вычислите синус угла.
2. Перемножьте между собой длины сторон.
3. Разделите величину надвое.
4. Умножьте друг на друга данные из пунктов 1 и 2. Результат готов.

На заметку! Запись данной формулы: 

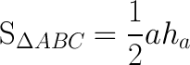
В примере с прямоугольным треугольником посчитать его площадь можно в три нажатия на калькуляторе. Достаточно перемножить значения его катетов (прилегающих к прямому углу сторон) и разделить произведение надвое.

Метод Герона

Античный математик Герон Александрийский предложил свой способ получения квадратуры треугольника. Для вычислений достаточно знать длину трех его сторон, хотя сама методика достаточно сложна и не поддастся пятиклассникам:

1. Определите периметр: сложите отрезки сторон: a+b+c. Разделите число надвое. Полученные данные называются полупериметр (p) и имеют ключевое значение в геометрическом уравнении Герона.
2. Проведите вычисление по формуле: p (p — a) (p — b) (p — c). Т.е. сначала вычтите по отдельности длину каждой из сторон из значения полупериметра, а затем перемножьте между собой три полученных числа и сам полупериметр.
3. Извлеките корень из итогового значения. Искомая величина найдена.

Например, грани длиною 3, 4 и 5 см образуют полупериметр 6 см. После умножения согласно формуле получается значение 36. Корень из 36 равняется 6. Значит, 6 см² — площадь этого треугольника. Для равносторонней фигуры расчет еще проще.

Вычисления с помощью окружностей

На практике используются способы расчета площади треугольника с помощью вписанной или описанной окружности. В первом случае необходимо знать величины всех сторон и радиус вписанного элемента. Далее:

• найдите полупериметр (p);
• умножьте полученную величину на значение радиуса (r) окружности и получите площадь.

По описанной вокруг треугольника окружности также можно вычислить его площадь. Потребуется знать радиус:

• получите произведение всех сторон треугольника;
• умножьте радиус на 4;
• разделите первое значение на второе.

Важно! Формула:

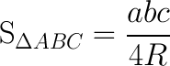
Пример для треугольника со сторонами 3,4 и 5 см. Если описать окружность, касающуюся каждой его вершины, то ее радиус будет равняться 2,5. После подстановки величин в уравнение получите итоговое значение 6 см².

Предложенный набор методов — базовый, но вовсе не исчерпывающий. Существуют более сложные способы решения задания с меньшим количеством вводных данных и многоступенчатым расчетом.